Utility
Everyone has preferences. In some sense it defines what being alive means and I tend to view preferences as axioms. They are also treated as axioms in economics. But what are preferences?
Formally preferences are a binary relation on the set of possible world states. The greater or equal symbol “≥” is such a binary relation for example and a good intuition for what we are getting at. We then make certain assumptions about this relation:
First of all we assume connexity (also called “completeness”). This just means that we can compare any two world states, which means that for any two world states A and B, we either “weakly prefer A over B” (A ≿ B) or we “weakly prefer B over A” or both. If both are true (we weakly prefer A over B and weakly prefer B over A), then we say we are “indifferent between A and B” (A ~ B).
For this reason we also require reflexivity, i.e. we always weakly prefer A over A for any world state A.
The last crucial assumption is transitivity which means that we weakly prefer A over C if we weakly prefer A over B and B over C.
These three assumptions are the base assumptions for ordinal utility. While this relation is very similar to the “greater or equal” (≥) relation, it is not the same. The crucial difference is that preferences do not have to be antisymmetric, which means that (A ≥ B) and (B ≥ A) imply equality (A = B). Because we can have two distinct world states we are indifferent in between without them being the same world state. For the same reason preferences are not a total order.
If the set of all possible world states is finite (or countable to be precise), then these three assumptions about the preference relation are enough to prove the existence of a utility function. A utility function $u$ assigns every world state a numeric value (real number) and has the property that comparing the numeric values of world states is equivalent to comparing two world states, i.e.
$$u(x)\ge u(y) \iff x \succsim y$$
In other words: a utility function transforms an abstract preference relation on world states into a greater or equal relation on numbers. This makes it a lot easier to work with.
Now it is important to note that the existence of a utility function does not mean that this utility function is unique. In fact adding a constant to a utility function does not change the ordering, so this results in another valid utility function. In fact any monotonous transformation of a utility function is still a utility function describing the same preference relation. This means that the specific number (the utility) which is assigned to a world state is meaningless by itself, because it is not unique. This is similar to how the number 10 is meaningless for measuring temperature without a unit (like celsius) to go with.

What is not meaningless are indifference curves (sets). Indifference curves are basically contour lines of the utility function. Think of hight maps where the circle of points on the same hight around a mountain are marked with a line, or isobars in pressure maps. While the the particular number assigned to these utility levels is pretty meaningless, the shape of these indifference curves are often enough to explain how trade works.
Of course in reality the set of world states is much more complicated than a two dimensional surface with a height. But if you imagine a world state being a vector with many different attributes, you can keep all those attributes the same except for two (what economists like to call “ceteris paribus” - “all things being equal”) and use this slice of all possible world states to create such a visualization. One might for example keep all attributes constant except for the amount of good X and Y a person possesses and get a height map like this.
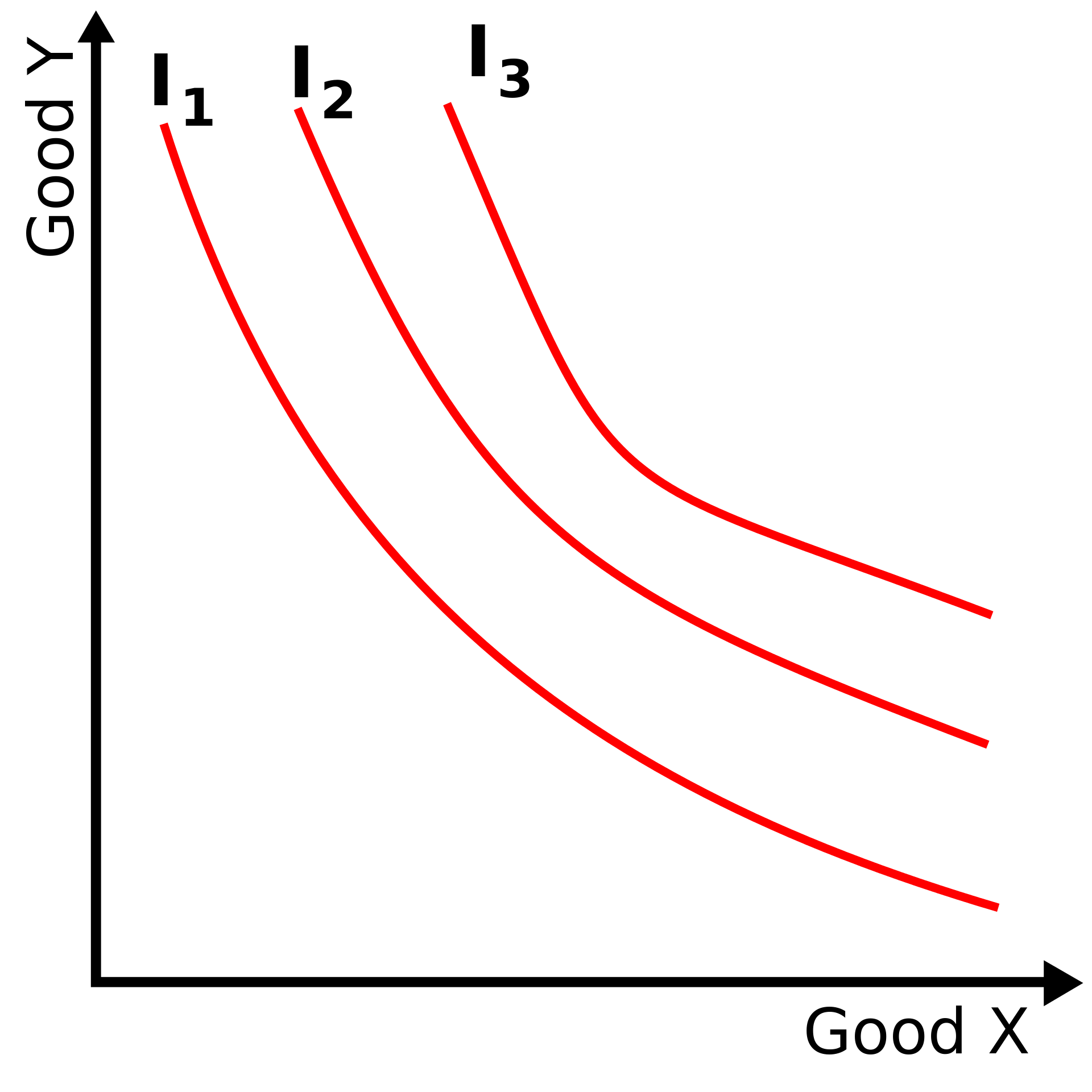
If we assumed for a minute that those lines would be straight, you could determine the slope of this line by selecting a point on the line, going left by one unit and going up until you hit the curve again. The length you need to go to up is the amount of the good Y you need to receive to make up for the lost good X because then you end up on the curve again (which is by definition the set of points you are indifferent in between). Now if the lines are not straight, they might still appear to be straight if you zoom in enough. This zooming in is basically taking the derivative and this ratio is also called the marginal rate of substitution. Around a particular point on the curve, you are willing to trade X for Y if you get at least this ratio of Y for X and vice versa.
As long as you do not end up in some corner case, where someone has already traded all X for Y (or Y for X), trades will continue to happen until the going exchange rate is equal to everyone’s marginal rate of substitution. This observation is the basis for the first fundamental theorem of welfare economics, which essentially states that an (idealized) free market (with perfect information, no market power, no externalities, etc.) will result in a pareto optimal outcome. Pareto optimal means that no individual can be made better off, without also making somebody worse off.
Note that Pareto optimality does not make any statements about fairness. It is more of a bare minimum to exclude a bunch allocations which do not even fulfill such a basic requirement everyone can agree on. Something like fairness is a much more difficult goal because it is very difficult to define and much more subjective. It would often require comparing utility functions or somehow summing them, which is not really possible since they are not unique. And if you want to make the preferences of someone more important you could simply multiply their utility function with a large number, then the result is still a utility function describing their preferences, but suddenly everything which makes them worse off results in really big utility differences.
In practice people usually solve this issue by evaluating everything according to their own utility function by imagining themselves in the shoes of other people and evaluating the impact of their actions according to their own preferences. This works as long as preferences are sufficiently similar. Everyone can relate to hunger, so people usually agree that it is “the right thing” to prioritize that over basically everything else for others as well. But people can not always relate to others preferences and that is usually where disagreements happen.
Combining the utility functions of many individuals into one preference of society of sorts is not only difficult, it can in fact be shown that it is impossible. This result is known as the Condorcet Paradox or Arrow’s Impossibility Theorem, where the condorcet paradox is more of a concrete example for weird behavior happening with different known voting systems while arrows impossibility theorem proves that there cannot be any voting system which has certain properties everyone would agree a voting system should have. PBS Infinite series made two excellent videos explaining those two results.
Since combining individuals utility functions into one social preference function for society is actually impossible economists usually stay away from fairness arguments. This might be surprising as it might seem that pareto efficiency should naively be a given. Everyone agrees that things should happen if it makes someone better of and nobody worse off. So it seems that the real problem should be making the world fair, as pareto efficiency should be easy. But this is in fact not the case. Achieving pareto efficiency is often not a given and in some cases even impossible.
In the following chapters we will encounter many such situations where there is no good solution to even achieve pareto efficiency let alone fairness.
Why Trade is Good
Economists generally like free trade - because restricted trade does usually not result in pareto optimal outcomes.
| Alice | Bob | |
|---|---|---|
| Cleaning | -35 | -30 |
| Cooking | -29 | -32 |
As an example imagine Alice and Bob share a flat together. They might randomly assign tasks like cleaning and cooking every week. Maybe Alice usually takes 35 minutes for cleaning while Bob only takes 30 minutes, and Bob takes 32 minutes for cooking while Alice only takes 29 minutes. Let us assume they do not have any preference for these tasks and the results are of similar quality for now. Then Alice will save 6 minutes if she swaps all cleaning tasks for cooking tasks, and bob will save 2 minutes if he swaps all cooking tasks for cleaning tasks.
Restricting trade in this scenario would make both worse off. So why would people ever choose to disallow trade? One reason Bob might not want to trade with Alice is, because he wants to learn cooking and if he never does it he will never improve. This is probably the main reason nations restrict trade they want to help a local industry bridge the knowledge gap, and while importing cheaper foreign products would be better in the short term it will also cause these local industries to die, preventing this knowledge acquisition in the long term.
Now one could of course ask: Why would Bob want to learn to cook if he can always trade with Alice? And the answer is already part of the question: “always trade” - who says that Alice will continue to trade with Bob forever? Bob might want to reduce this dependency on Alice. This dependency is could become a problem for two reasons: Alice may not be able to trade, or Alice may not want to trade any longer.
Countries are very careful for example when it comes to food and water imports since their trade partners would likely prioritize themselves if shortages would occur. But they are also careful to not be too dependant on other countries since they might use this dependency to their advantage. Trade sanctions are the modern way to exert pressure after all. All these considerations make sense but still result in an outcome which is not pareto optimal.
Nontrivial Exchange Rates
| Alice | Bob | |
|---|---|---|
| Cleaning | -5 | -3 |
| Cooking | -30 | -33 |
At the moment we are only trading one task for one, but what if cooking takes significantly longer than cleaning? Then trading one for one is not in Alice’s interest anymore. So what would Alice accept? Well in order to break even, Bob needs to offer to clean at least 6 times for every time Alice takes one of Bob’s cooking responsibilities. On the other hand Bob will stop accepting the exchange once he has to clean more than 10 times in exchange for not cooking once. So what is fair? 8 because it is in the middle? But then Alice gains 10 minutes by exchanging 40 minutes of cleaning for 30 minutes of cooking, while Bob only gains 9 minutes by changing 33 minutes of cooking into 24 minutes of cleaning. So should we optimize for that?
Or should we minimize the amount of minutes spent on housework in total? That would mean trading everything which results in a one for one trade which is very disadvantageous for Alice.
Now for a pareto optimal solution it is enough if Alice does not have any cleaning tasks left because then her situation can not be improved without making Bob worse off. And that will be the case no matter if the exchange rate is 1,2,… or 10. The question is just how many cooking tasks Bob will have left after the exchange since anything but one for one trade will leave him with cooking tasks left over. So if they just bargain, they will end up with an exchange rate between 6 and 10 which has such a result, so most economists would call it a day.
Comparative advantage
| Alice | Bob | |
|---|---|---|
| Cleaning | -5 | -3 |
| Cooking | -40 | -30 |
So what if Bob is faster with cleaning and cooking? Then Alice might still have a comparative advantage for cooking for example. In this example she would be willing to trade 8 cleanings or more for one time cooking whereas Bob would trade one cooking task for at most 10 cleaning tasks. So they can still trade. And this trades makes both of them better off even though Bob is faster at both of these tasks.
Now if we wanted to minimize the absolute time it takes to do the housework, then Bob should do all of it. But in a free trade situation, that is not what happens. Trade still reduces the amount of housework in total. It just does not minimize it. But at some point the only way to reduce it further is to give Bob more of Alice’s work so that point is already pareto optimal since that is not in his interest. And such a point is reached in free trade.
Alice has, what is know as a comparative advantage when it comes to cooking. While she is not in fact faster at cooking than Bob (Bob has the absolute advantage) she is faster at cooking when cooking is compared to cleaning. This concept first discovered by David Ricardo is an explanation why more developed countries (with machines making both tasks faster) might still trade with developing countries for hand made products.
| Machine | Hand | |
|---|---|---|
| E | -1/100 | -1 |
| H | -9/10 | -1 |
For further illustration consider a product which is easy to automate E, and a product which is difficult to automate H. Let us say that it takes an engineer 1000 hours to build a machine that builds 100,000 items of product E before it breaks down and it takes 90,000 hours to produce a machine that builds 100,000 items of product H. Hand making these products takes 1 hour per item in both cases. Then product H would cost 90 times as much as product E in a developed nation without trade since the average time required per unit is 90 times as high. But since these goods trade one to one in undeveloped nations, they would be happy to trade H products for at least one E product. From the perspective of a developed nation, they can get product H for “dirt cheap” from an underdeveloped nation.
Now here is the thing: Any price between 1 and 90 will result in trade and a pareto optimum. But a price of 1.1 will barely improve the situation of the developing nation while greatly reducing prices in developed nations. This might be viewed as exploitative for obvious reasons.
But notice that preventing trade altogether is a poor solution, since that does not improve living conditions in the underdeveloped nation at all. Trade still improves the conditions for both parties. The question is just by how much?
Ultimatum Game and Bargaining
So why would the price be so skewed towards one or the other side? A first approximation is the ultimatum game. In this game played by two players, player one makes an offer how a pot of money is distributed between the two. The second player can only accept or reject. If the second player rejects the offer no one gets any money. From a rational standpoint, people should accept any offer above zero. They get money for free in that case it should not matter how much money somebody else gets. And given that player one knows this, the optimal play for them is to take everything assuming a rational player two.
In experimental settings people did often offer a 50:50 split and offers below 30% were often rejected. There is an ongoing debate why this is the case. It seems that higher stakes reduce rejection rates for example1. I would also guess that not telling player two how much the initial value and the share offered was, and only telling them the amount they would get would change a lot. But that is not really the point here.
So if you are a corporation and make an offer for a wage, you are kind of player one, so is such an “unfair” split really surprising? Especially since the free market is specifically designed to apply evolution to corporations leaving only the most efficient and rational ones to survive. Now in reality such a game might sound extreme since people could always make a counter offer. To model this slightly more complicated situation Ariel Rubinstein came up with a bargaining model with an infinite time horizon, where players can make offers and counter offers to split a sum. But the total amount to split decreases over time with a discount factor. This discount factor might represent the cost of not coming to an agreement for some time. This forces the minimal offer to be accepted to be higher. But this minimum is closely linked to the discount factor.
Now if we would generalize this again and assume differing costs for a delayed agreement and thus different discount factors, it is quite intuitive that the person who needs the money to feed themselves will be much less patient than the party which can wait. This difference in bargaining power results in very skewed distributions of the surplus. Multiple people bargaining games are also discussed in economics, their maths becomes much harder but power does generally fall towards the side with fewer entities on. I.e. the ability to take your business elsewhere generally grants bargaining power.
Unions, unemployment benefits to fall back on, wage transparency, etc. all increase the bargaining power of workers without setting fixed rates like minimum wages. Although unemployment benefits fail to increase peoples bargaining power if they are conditional on accepting any job offered, since that essentially forces people to accept any offer. So that might actually decrease bargaining power. Unconditional Basic Income (UBI) on the other hand would give people the ultimate “F*** you, I can walk” card, which makes it quite attractive in my mind. But it might overshoot and actually result in a lot of unemployed people which could then mean not enough taxes to support the scheme in the first place. And if UBI might get taken away at any moment due to being too expensive by the next administration, it does not actually have the desired safety net effect. So I am not completely sold yet.
You might remember me asking, whether the price should be just the median of the possible interval or the price point where both parties gain the same number of minutes. And while the pareto optimal solution seemed good enough then, you might insist on a more specific solution now. Some might now even have the opinion that the surplus should be distributed with a bias towards the poor. That is a nice notion. But it does not really work. Not only are these benefits hard to calculate in reality, they are often impossible to calculate. To see that, we have to circle back a bit.
Introducing Utility to Trade
At the beginning of this chapter we assumed that Alice and Bob would not care about the task and only care about the number of minutes. This is generally unrealistic. So now we have to generalize this notion. But since we want to keep the maths light we will instead assume that they will take the same amount of time for every task. So why should they trade? Well maybe they prefer one task over the other. And if they prefer the opposite tasks, they can still trade.
Now as I argued in the utility chapter assigning utility numbers to certain world states is quite arbitrary, but the indifference curves (sets) are not. And while the marginal rate of substitution is only really defined very locally we will assume for simplicity here, that if Alice is happy to swap cleaning for cooking 2:1 in some world state, she will be happy to do this exchange in any other world state too. This means we assume linear indifference curves.
This is not realistic if people like variety for example, then it depends how many tasks of a particular type they already have when they decide whether to trade them. But for the point I am trying to make such a complicated utility function would only make things difficult to understand.
| Alice | Bob | |
|---|---|---|
| Cleaning | -10 | -4 |
| Cooking | -2 | -10 |
So here is a simple example. This times the number do not represent minutes but utility. But similarly to before, Alice can simply swap her cleaning tasks for Bob’s cooking tasks and both would be happy. But what if we modify those utilities a bit. What if Bob does not actually dislike cooking all that much?
| Alice | Bob | |
|---|---|---|
| Cleaning | -10 | -4 |
| Cooking | -2 | -2 |
In this modification Bob would not want to trade away a single cooking task for a cleaning task. So this trade would not happen. But he would be willing to trade away two or more cooking tasks for one cleaning task.
Alice on the other hand really dislikes cleaning so she is willing to trade up to 5 times cooking for one of her cleaning tasks. This means there is still a range where both parties would be willing to trade. But the rates would have to be between 2 and 5.
And here is where the issue lies: there is no difference in preference for Alice in the first example and the second example. But in one case she trades a cooking task one for one and in the other case one for two or more. Now Bob from the first example might get the idea to present as Bob from the second example to get this improved conversion rate. There is no way for Alice to tell the difference since we are strictly talking about preferences which are completely subjective.
And for this reason Alice in the second example might refuse a 2:1 trade because she distrusts that Bob is telling the truth about his preferences and wants to avoid getting screwed over. So Bob with preferences from example 2 might not even offer this exchange even at 2:1 (which would not benefit him at all and only leave him indifferent), because he does not want to come across as greedy.
So people sometimes avoid trade to avoid social drama even though this trade would in fact make everyone better off (constitute a pareto improvement). And since preferences are hidden, trying to balance the benefits is a completely hopeless endeavour.
And we have excluded different levels of quality/effort completely from the equation until now. Whoever thinks that letting an external observer assign payoffs is fair in any way, has never been part of a group project.
Fair Wages
And corporations are really just big group projects. In the beginning you do not have any money so you split (ownership) shares equally (or try to balance them based on contributions). People who join later will at first likely be compensated with stock options as well, but gradually the share of the wages in the compensation package will increase. And here is the thing, equity is a lottery ticket. Most of the time startups fail, but some of the time they take off. Sure stocks will suddenly be worth a ton which is probably not a fair share of the work they did. But the amount of money lottery winners get is also in no way proportional to the amount of money/work they put into it. But you still can not take that win away - otherwise nobody will play the lottery anymore. More on that in Risk.
But the funny thing is, that the winners of that lottery tend to attribute their success to their own genius and hard work and overlook the amount of luck they had. Additionally they get used to having money. Both of these factors likely makes them quite confident in negotiations which means that company leaders continue to take a large percentage of the surplus even after the company becomes established and the risk is a lot lower. This in turn means that it becomes common practice to pay a lot for leadership positions, which gives ammunition for comparisons in salary negotiations further cementing extremely high salaries for leadership.
Money
Before we get to risk, I want to touch on money to make examples easier. So what is money? To answer that question let us get back to our flatmates Alice and Bob. Now let us assume they have a system where they just deal with housework as it comes up (e.g. trash is full), take care of it and entry the time it took into a ledger. They want to have an equal partnership, so they want to keep track of the difference. For this reason they tally up the total contributions from time to time.
They use this system for quite some time and the numbers get bigger and bigger. But since they have approximately contributed the same only the lower digits really matter. The current state might be something like 1034 and 1038. They then decide to just remove 1000 from both tallies to make the numbers shorter again.
To save rent, they end up adding Charlie to the flat. Now at some point Bob notices that the washing machine is finished and hangs up Alice’s clothes. After he finishes he walks to the ledger and starts to write 10 minutes in his column. But then he pauses and realized that this action did not benefit Charlie and if he would increase his tally, then the difference between them increases so Charlie would be required to do something to make up for that at some point.
After a discussion, the flat adds 5 minutes to Bob’s tally and removes 5 minutes from Alice tally. They reason that now the difference between Bob and Charlie might increase by 5 minutes but the difference between Alice and Charlie decreases by 5 minutes which means Charlie is unaffected by this change in total. The difference between Bob and Alice on the other hand increased by 10 minutes which is exactly the time Bob spent on a task for Alice.
In the future they know how to deal with person to person transactions. Simply add half to one account and subtract half from the other account. If we sum the total amount of time between all flat members, then a person to person transaction does not change this total amount.
Now it is pretty easy to see how this is pretty much equivalent to fiat money. The group as a whole can simply print it or take it out of circulation by removing e.g. 1000 from everyone (which is what taxes can do). While individuals can only exchange it.
National Debt
Now the amount of debt the group (state) has does not really matter, but it does matter how the money distribution looks. If everyone has 10xx amount of money, then the state can easily reduce the amount of money in circulation by reducing the balance of everyone by 1000 leaving them all with xx. But if just on person has a ton of it, this debt reduction becomes more difficult. Because you can not just take 1000 from everyone now, because the other people do not have that. Now the rich person might be scared that the group might just default on them. So they might stop valuing the amount they have at the actual minute face value since there is a probability they will never get that back. So the value of their money decreases.
They might be willing to spend 20 minutes of “ledger money” to get someone to do 10 minutes of work. Because then they get at least 10 minutes back and they are not sure if they would see any of it if they continue to have so much in comparison. What is happening is inflation.
Now in the real world you can not see everybody’s balances, so how can inflation be tied to inequality? Well you can not continue to spend (interpersonally) once your balance reaches zero, so the inequality is capped by the amount of money in circulation. If you increase this amount of money in circulation then you increase the cap on inequality, since now people can spend this additional money until they are at zero again resulting in a larger difference.
Now the time where these inequality problems become most apparent is when you try to slash the money in circulation. Because at that point some people might just be too poor for that. For this reason the money system is generally more stable, if you never actually change the amount of money in circulation. Instead the group stops financing group projects by issuing money and finances them by taxes directly (i.e. move the money slashing together with the spending).
In reality one can of course go below zero when it comes to money. But since going even lower increases the spread further and increases the chances of default, this “going below zero” is only possible when someone vouches for you. I.e. gives you credit. You can then go below zero, but if you can not repay that money your creditor has to balance your books. Now to avoid the creditor vouching for too many people, you kind of have to mark the money they used for vouching. For this reason credit is generally structured such that the creditor hands over money to the debtor and gets an IOU for this money.
Anyway, this means that the real national debt is actually the “national debt” plus the amount of money in circulation. And money is nothing but debt. This also means that anyone can really issue money - it is called a coupon or IOU. But debt issued by the entire group (nation) is just more reliable and universally accepted than the coupon for an ice cream at Joe’s lemonade stand.
Money Supply and Velocity
Assume that Alice likes to do housework in the beginning of the week while Bob likes to do it at the end. They started to use a group account to avoid issuing money all the time and this group account is filled by taxes at the start of the week. Assume that the group account is at 60 at the start while Alice and Bob are at zero. Alice does her housework in the beginning of the week leaving her account at 30 in the middle of the week, the group account at 30 and Bob’s account at 0. In the end of the week Bob does his tasks and earns the other 30 from the group account. Then at the very end of the week both are taxed 30 and the next week starts.
So now Charlie joins the flat. Since an additional person is causing dirt and thus housework, the budget of the group should to increase. But the budget is already the entire money quantity. So taxes can not be increased above 60. Alice suggests to continue spending 60 for now as they do not have a better idea. They reason that the taxes are going to be 20 at the end of the week, so they know that they should do 20 minutes of work each. At that point Bob argues that he already made a time slot for 30 minutes and that they could just entry 2/3 per actual minute. Then everyone would work 30 minutes but they could still work with only 100 money minutes in circulation.
What just happened is called deflation. The value of one unit of money is now worth 1.5 actual minutes of work. Now in reality people do not sit down together and decide for deflation to happen, but the mechanism is similar. The quantity of money is not enough anymore to support the number of transactions necessary. This means that the production capacity of some companies is unused. To avoid this under-utilization they reduce prices. The opposite happens when there is too much money around.
So how much is the right amount if we want price stability? To answer that question, notice how the nominal GDP (the sum of all transactions) per week is roughly equal to the total amount of money here. Because money is used roughly once per week and then reused. The number of uses is the money velocity multiplied by the total money supply is necessarily equal to the nominal GDP. The real GDP is the actual minutes of work done per week. The price level multiplied with the nominal GDP is equal to the real GDP. So if we want to keep the price level stable we have to keep the nominal GDP equal to the real GDP. The money velocity is generally determined by things like wage cycles, tax cycles, etc. and thus not easily (sensibly) influenceable. So the sensible thing to do, is to adjust the money supply to the real GDP if one wants stable prices.
Now some might question why stable prices are desirable. And the answer is pretty much fairness. If you worked 2 minutes to get 2 credits, it is only fair if you can exchange those 2 credits for 2 minutes of work in the future. Inflation takes away value from these credits, deflation adds value to these credits. For this reason I find deflation much worse than inflation, since deflation adds value to existing wealth increasing wealth disparities while inflation works more like a wealth tax (although note that it only taxes actual money and not other forms of wealth). For this reason I find a small predictable inflation rate to be optimal. It is a constant force eating away at inequalities stabilizing the monetary system which is destabilized by these inequalities. But it is not large enough to be relevant to normal money use (i.e. use which does not consist of hoarding it).
This is the main reason I am skeptical of “proof of stake” cryptocurrencies still. While they solve the abhorrent energy use problem of “proof of work” crypto, they still plan on a fixed money supply independent of the GDP. And since the real GDP tends to grow, this naturally results in deflation. In fact the entire “investment promise” of crypto is, that more people will join (thus increasing “its GDP”) making existing holders rich by deflation. That is not a healthy. The gold standard has the same problem and its supporter seem to be from a similar crowd.
Small Excursion on different Money Supply Levels
As already mentioned the restriction that your balance can not drop below zero is somewhat lifted by credit. The creditor basically vouches with their own money for the debitor. The debitor can use the money the creditor provides while the creditor receives an IOU which is basically money too, since money is just credit. In the real world most people have their money in a bank and allow it to lend out its money (i.e. act as creditors).
Now assuming that everyone would have their money in the bank, the bank lends out the money this money is then deposited into the bank which means it can act as a security to vouch for some other creditor again. This means that money is lent out multiple times creating many IOUs in the process. Since the IOUs (the account balances of the banks) are treated like money and generally outnumber “actual money”, they are called the level 1 money supply (M1), while the “actual money” (i.e. central bank issued money) is called M0. There are additional increasingly large volumes of money supply with decreasing amounts of liquidity.
To keep M1 in check banks can not lend out the full quantity of money deposited and have to retain a certain reserve percentage. This reserve requirement was reduced in 2012 from two to one percent in the european union for example.
Central Banks often do not actually adjust the M0 money supply and try to adjust the money supply by influencing the M1 money supply. This can be achieved by adjusting interest rates which in turn adjust the amount of borrowing happening which then influences M1.
I am not sure why to be honest. It seems much more effective to stop trying to decrease interest rates and actually print money if decreasing interest rates fail to work (as they seem to). If people do not want to borrow more you can not force them to.
Risk
Our ordinal utility function has served us well until now. But in order to deal with risk we need to make more assumptions. To assess risk, it is also important to ask “by how much better?” and not just “better or not?”. To obtain such a cardinal utility function we first assume that we do not only have preferences over world states, but actually preferences over probability distributions over world states. Now here is the thing, if we have two probability distributions and one happens with probability p and the other with probability (1-p), then this setup itself is a probability distribution over world states too. The property we would like our utility function to have now, is that such a combined distribution
$$px + (1-p)y$$
of the two distributions x and y has utility
$$u(px + (1-p) y) = pu(x) + (1-p) u(y)$$
Such a utility function is called cardinal utility and is unique up to linear transformations (shifts up and down and multiplying the function with a constant are still valid). The Von-Neuman-Morgenstern utility theorem states that the following additional assumption on the preference relation is sufficient for the utility function to have this property
For any world states x, y, z with $$x\succsim y \succsim z$$ there is a p between 0 and 1 such that $$px + (1-p)z \sim y$$ which essentially just means that there exists a probability such that you are indifferent between the mediocre world state and the lottery between the good and bad world state.
Recall that we already assumed connexity,transitivity, and reflexivity. This is not a very strong assumption either. And note that we were only able to construct an ordinal utility function on finite (or countable) sets of world states. Using the assumption above lets us construct cardinal utility functions on arbitrarily large world state sets.
But since linear transformations of utility functions are still valid cardinal utility functions for the same preference relation, utility functions are still not comparable under this new assumption.
Risk Aversion
| 0 | 100k | 1 mio | |
|---|---|---|---|
| utility | 0 | 500 | 1000 |
Many people misunderstand the linearity of the utility function with regards to probability to mean that people should be indifferent to risk and only consider the expected value. This is not the case. In fact it is a very common assumption in economics that people are risk averse. Consider for example a lottery where you make nothing 90% of the time and 1 mio € 10% of the time. The expected value is 100,000 € then. But if the utility for the guaranteed prices would be as in the table, the value of the lottery would just be
$$ u(0.9\cdot 0 + 0.1\cdot\text{1 mio}) = 100 \le u(100k) $$
which is considerably lower than the utility of the expected value. In fact a function with the property
$$ u(\lambda x + (1-\lambda)y) \ge \lambda u(x) + (1-\lambda) u(y) % = u(\lambda\cdot x + (1-\lambda)\cdot y) $$
is called concave. And functions with a decreasing slope are concave. This means that decreasing marginal utility is equivalent to risk aversion. In other words: If the improvement from 0 to 1 mio € is bigger than from 1 mio € to 2 mio €, then you “the increase” in utility decreases with wealth (i.e. your marginal utility goes down). And in that case it is rational to be risk averse. This means that most people prefer to take the sure expected value rather than the lottery.
This is the reason insurance exists. By pooling money, the lottery averages out. Nobody has to pay really large sums of money to cover an accident by chance, instead everyone pays a little bit for sure. Now insurance has operating costs so people have to pay a bit more than the average damages. But since they strictly prefer to pay average damages over the lottery, there is some wiggle room to accommodate fees and still improve everyone’s lives. To quantify this wiggle room, economists define the risk premium. Which is the additional amount of money one has to give a risk averse person to make them accept the lottery over the safe value.
Not everyone has to be risk averse, and there are local situations where a lot of people might not be. A good example might be, that you have the option between a lottery for two tickets and one ticket. Since you would enjoy the show a lot more with company than alone, the second ticket might be worth more than the first, which would make you risk loving in this case.
Lotteries are an easy way to introduce risk. So in that sense lotteries are the opposite of insurance.
Patience
Most people are impatient. If you are given the option for 1000 € now or in a year, almost everyone would take now. In part this is due to the fact, that you can always keep it til the next year. So getting it now must be at least as good as later. But additionally it also provides you with additional options you can do right now. Economists like to model impatience like this. They assume that you have basically the same preferences next year (which is probably reasonable to assume, since that is probably what everyone assumes about themselves), and then they argue that the utility of this year is the immediate utility of the things you do this year x0 plus the utility of what you do next year x1 with a discount.
$$ U(x_0) = u(x_0) + \lambda U(x_1) $$
To extend this to more than two years, the argument goes like this. We assume the preferences stay the same over time so the utility at timestep 1 is
$$U(x_1) = u(x_1) + \lambda U(x_2).$$
So if we now plug that into the first formula we get
$$ U(x_0) = u(x_0) + \lambda u(x_1) + \lambda^2 U(x_2). $$
Continuing with this line of argument we get
$$ U(x_0) = \sum_{k=0}^\infty \lambda^k u(x_k). $$
In other words we assume that the utility value of successive years decays exponentially.
This assumption is wrong. Experiments show that the discounting for the first year is much higher than for the following years. This means that in year zero a person assumes they will care more about year two in year one than they actually will, which results in procrastinating behavior. A more fitting discount method is thus hyperbolic discounting which is studied in behavioral economics. But since this way of discounting results in time-inconsistent behavior (people break their own plans), people often try to take measures which locks them into their plans. If we assume that people take these “rational guardrail” measures when making financial decisions it is probably fair to assume exponential discounting in investment theory. Lock-in might consist of a fixed savings plan, etc.
Exponential discounting also makes the math easier. Which is good for an introduction.
Investment
If your discount factor is 90%, then you would be indifferent between 9€ now, or 10€ a year later. If someone else has a discount factor of 95% they would value those 10€ later at 9.50€. So if you will get 10€ in a year, you could sell these 10€ in the future for 9.20€ now to this second person which would make you both better off. Receiving 9.20€ now and paying 10€ a year later is equivalent to taking out a credit with an interest rate of roughly 8.7%. And if you have a discount factor of 90% an interest rate of 11.1% makes you indifferent. Given a discount factor of 95% an interest rate of 5.3% makes them indifferent.
Since everyone can trade with everyone, available interest rates can in some sense be viewed as the result of averaging the “indifference rates” from all participating people which are a result of their individual discount factors.
There are a couple more complications like the fact that lending interest rates are often not equal to saving interest rates and people can not borrow arbitrary amounts of money. People usually do not lend out money to other people for them to use it for consumption. Because if people were going to borrow at these rates due to very high impatience, then they are likely to delay repaying this credit as long as possible.
So a different view to deduce interest rates is an equilibrium of available investments. Assume that you could buy a machine for example, which makes your work easier. Let us say it makes you twice as productive the next year but costs you time to build this year. Without the machine you might be able to produce goods of value 10 this and next year. With the machine you might only be able to produce goods of value 1 this year, but due to the doubling in productivity you can produce a value of 20 next year. Now if we want to compare those two scenarios we somehow have to determine a total value over all years. But as we already established, returns in the future are less valuable than returns now. So one has to discount the future year. Now we are indifferent between both scenarios if
$$ 1 + \lambda 20 = 10 + \lambda 10 $$
which is the case for a discount factor of 90%. In other words this investment opportunity is equivalent to an interest rate of 11.1%. So if you need funding to cover your first year of being unproductive while producing the machine, you can offer this interest rate at the maximum. In reality many different projects are funded. Investment projects are willing to accept different types of interest rates. If you sum all projects which are wiling to accept an interest rate of r and plot this number of projects against r, then the number of projects will decrease with r. On the other hand people who are willing to delay their consumption and provide the funding if they get an interest rate of r is going to increase as r increases above their indifference interest rate of more and more people. At some point the demand for funding equals the supply for funding which is the equilibrium interest rate.
In short: People more patient than available interest rates will provide funding at these rates for projects which yield at least these rates. While people less patient than these rates will generally not save money, but are also not able to borrow, because they are likely to still be impatient in the future and thus never really willing to pay it back.
Note that hunger generally reduces patience - patience might be determined by circumstances more than anything else and should not be viewed through a moral lense in my opinion.
Companies
Risk Reduction
For now we have ignored risk. We have to add that back in, since that is usually a large part of investments. Since we assume that people are generally risk averse we can assume that it is best if we can reduce risk.
If you were a trader in the middle ages for example you might buy a ship yourself and hope it returns from its trade trip. Alternatively you can group together with other merchants and buy multiple ships as a group. Now ships returning becomes statistic and the risk goes down. You then simply call this group a company and everyone receives “shares” of this company according to the money they contributed.
But even with this bundling of risks there will still be risk left over at the company level. Now you could buy shares of different companies to balance out risk even more but even then you will be left with systemic risks which affect the entire country/world.
So additional to the interest rates to balance out impatience, interest rates for risky projects are higher not only to yield higher returns in the case of success to balance out the low returns (or losses) in the case of failure, but also to provide a risk premium (which is necessary to make risk averse people invest). Due to these risk premiums one should expect that the group of relatively risk loving individuals (still risk averse but less than others) will be richer on average. But their wealth will also have a larger standard deviation.
So there are three things which make you stupidly rich: patience, appetite for risk and luck. And these are usually the attributes of self-made billionaires. They traded free time and comfort in the beginning (starting in a garage, long work hours, sleeping in the office, etc.) for lottery tickets (stock in a company) for future wealth.
They are especially risk loving since they can not even diversify. They actually only hold stock of their own company for many years.
Liquidity
So you invest into a company and receive stock in return. But what if the company only makes profits in two years and you need the money in one year? Here the stock market comes in. Because somebody else might be willing to delay their consumption in the second year - so they can take over the investment for you. They then buy the stock from you - at a higher price because they do not have to wait two years till the payoffs anymore. Company shares thus allow people to decide how much and for how long they want to invest and companies to decide how much and for how long they need the money somewhat independently. Because the underlying money can simply be exchanged.
But since expectations can change very quickly and the worth of a company is simply the value of their expected future returns their value can swing wildly in the short term. So you might not always be willing to buy or sell which means that stock is still less liquid than a bank account with fixed but lower interest rates.
Competition
In Why Trade is Good I already argued why determining a fair wage is really complicated. A wage is the product of a negotiation taking into account minutes worked, quality of work (also influenced by past investments into education), preferences for different types of work and lastly bargaining power. Now it is unfortunate that bargaining power plays such a huge role in determining wages, but we already discussed that, and I am not aware of any way to fix that. But additionally it is really a separate issue.
So for now let us just assume for simplicity that everyone is equal and earns a wage proportional to their amount of work. Since they exchange their work minutes one for one in this case (again look at introducing utility to trade for generalization), the sum of work minutes needed to produce a good determines the price (i.e. the number of work minutes) the buyer has to give up in exchange for that good.
It should be quite obvious that the price should not be lower than the sum of work minutes needed to produce the good, otherwise people would buy it which would not be willing to give up that much free time for it which is not sustainable from a global perspective if people exchange their time one for one. Similarly the price should not be higher than this cost, otherwise people who would be willing to expend the effort needed to produce the good could not get the good which makes them worse off than they need be.
So what we want is two things:
- Costs should be minimized (find the production method which minimizes the work minutes needed to produce something - assuming constant quality)
- Prices should be equal to unit costs to guarantee a pareto optimal production quantity where only (all) the people willing to expend the effort to produce the good actually receive the good
The Trouble with Fixed Cost
These are the necessary requirements to ensure pareto efficiency. Before we discuss how to achieve these goals, let us first touch on what is included in “costs”. Until now I hand-waved it to be the sum of all work minutes needed to create a product. But if we look a bit closer many production processes have an initial investment part and a production part. The initial investment involves developing the process itself and building machines if appropriate.
As we have already argued, investment is not free (you have to pay someone for the money - i.e. to delay their consumption) and the risk that the development does not pan out has to be covered as well. So you will have to pay interest on money investors provide. These are “capital costs”. In the real world capital costs can be interest on credit or dividends you pay shareholders both are capital provided by investors, although credit has less risk involved so interest rates are usually lower than dividend payments per share on average (averaging over multiple companies and time). The second component is labour costs which are self explanatory.
Now while machines will eventually break down and thus produce only a limited amount of products, development of the production process is truly a one time effort. So we have to make a difference between fixed costs and variable (or marginal) costs.
A good question you might now ask is: should the price be equal to the variable costs or the average costs (including the fixed costs)?
The answer to this question is tricky. On one hand the production costs have to be covered. So if everyone pays the average costs production costs are just covered. Variable costs on the other hand do not include fixed costs and are thus lower than average costs. So if prices were equal to variable costs, the total costs could not be covered.
But if the price is above the variable cost, then the life of a person who would be willing to pay less than the price but more than the variable cost could be improved without making a loss. This means that any price above variable cost is not pareto efficient.
There are two solutions to this problem. The first is price discrimination i.e. asking for different prices from different people. Now the average price charged still has to be equal (or larger) than the average cost. Which means that in the limit every, single person has to pay exactly their willingness to pay if that just covers all the costs. This is of course not realistic in the real world.
And while corporations already discriminate on occupation (e.g. student discounts), discrimination based on IP address or similar is generally viewed as creepy. So there are limits to what is possible there.
So what is the other solution? The other solution is that the fixed costs are payed for by somebody else than the corporation. Maybe everyone pays for it through taxes. This means that some type of product is subsidized by people who do not necessarily want that though. If you just want to achieve pareto efficiency this is not a problem. Taking away something to gift somebody else does not prevent you from achieving pareto efficiency. But it is still questionable whether that is ethical.
Additionally there are practical problems:
- How do you determine the size of the fixed costs from outside the company? If you simply ask the company, it has huge incentives to exaggerate them.
- How do you determine which companies to fund? If you fund everyone then you end up with a ton of companies (each on of them with potentially huge initial costs) which might sell very few products - not exactly cost minimizing.
So both approaches do not really work. So what options do we have?
Minimize Cost
If multiple companies offer the same product and the price is larger than the average cost, then it makes sense for a single company to slightly reduce the price which reduces their income per product only slightly but massively increases the number of products sold as they undercut everyone else. But since ever other company has the same incentive they will try to do the same and the companies bid lower and lower until they hit the average cost floor.
This simple model is called Bertrand Competition. A more sophisticated model is Cournot Competition which takes into account one can not just see the price of a competitors product and immediately undercut them because you can not magically conjure up all the devices you would sell when you undercut their prices. So instead of optimizing over prices, companies determine a quantity of products they produce beforehand. And when they produces these the price will fall until all of them are sold. This does not necessarily mean that the price falls down to average cost.
But as the equilibrium price in Cournot competition decreases with the number of firms participating. And companies will enter the market until the next entry would reduce the price below average cost. But the price can be considerably above the average price before this entry. Potential founders just know that there is not any space left for an additional company.
Since the next entrant would move the price below average cost, it is probably fair to assume that the price was already close to average cost (although there are probably examples for extreme cases where this is false).
Now if variable costs are high and fixed costs small, average costs are roughly equal to variable costs. This means that the price variable cost equality is almost satisfied. And if someone has an idea for a production method with lower costs, they can always create a company out-competing the existing companies with lower prices. And even if nobody entries the market, the potential for competition keeps companies innovating to preempt these entries.
But if fixed costs are high, the spread between average can variable costs is high, which means that many people do not buy the product even though products could be made for them at a price lower than what they ware willing to pay. And additional to this problem, the number of companies in the market will be small, because every company that enters considerably increases the average cost since the average cost consists mainly of fixed cost. In the extreme case there are no variable costs (e.g. software) and only one company offers the product. If another company now enters the market the total costs of the entire industry will double (two times the fixed costs) and if the prices do not go down enough to also double the number of consumers, the average costs will be higher since twice the cost have to be divided through less than twice the number of consumers. So not only does the price go down but the average costs also increases. This means that this entry could actually move average costs above the price in one big movement.
This means that the second company would never enter, even if the monopoly asked for a price like double the average cost.
In other words, when fixed costs are high:
- prices are too high resulting in a loss in pareto efficiency due to people not buying who would buy at lower prices and
- companies make profits beyond profits covering capital expenditure (compensation for consumption delay and risk). Note that both are accounted as profits (accounting profit) and the surplus profit (beyond fair compensation for delay and risk) is called “economic profit”.
- since only very few companies will remain in equilibrium (due to high
fixed costs) capital expenses due to risk are very high because most startups
in this space will fail as only few companies will remain.
This also explains the extremely high price to earnings ratios and high profit margins in the tech stocks. And since fixed costs keep rising as more and more things are automated I expect PE ratios and margins to continue increasing.
What could possibly go wrong?
Competition is an evolutionary algorithm for cost reduction. It will do exactly that. Whenever you create an algorithm for minimizing something you should be very aware of unintended consequences since the minimum might not have the properties you like. E.g.
letting students optimize their grades does not necessarily result in optimal learning. They will take shortcuts if you make them available
letting a reinforcement learning algorithm maximize points in a boat race might result in the algorithm collecting boost spawns at the side of the race instead of actually winning the race2.
it is therefore critical to understand what minimizing costs might look like. If this minimization process might cross lines you would rather not have crossed you should create regulatory restrictions there. Companies might also not take into account external costs. Emitting CO2 causes somebody else costs but not the company itself, so it is not taken into account. By creating a tax on CO2 the company actually has to take these emissions into account and the optimization algorithm works again.
The process of taxing companies for causing external costs is called aptly “internalizing the externalities”. Whenever such externalities are discovered taxes equal to these externalities should be implemented to internalize them. If that is done the optimization algorithm works properly. Whenever you have to ask consumers to ignore this optimization algorithm and not buy the cheapest product, the state has not done its job, of properly specifying the optimization problem. In some cases it is difficult to estimate these external costs. This is the case for CO2 as well. In that case one can use certificates instead. They work quite similar to taxes but set the total quantity instead of the cost (see Why Certificates are the Right Tool for Limiting CO2 Emissions).
There are also sectors where there is not much room to optimize but many ways to cut corners you do not want cut. In nursing the only cost is working minutes of nurses. So the only way to cut them is to reduce their working time per patient (or reduce their wages) - or build nursing robots. But since nursing robots are still far in the future, do you really want to let an optimizer lose on a problem you know there should be no way to reduce costs of? Because any cost reduction this optimizer finds is bound to be unintended.
Other Options
I stated multiple reasons above, why you might be unhappy with a free market. So what are alternatives?
Planning/State owned Enterprise
Advantages
- Price can be set equal to average cost or even variable cost and fixed cost funded by taxes
Disadvantages
- No incentive for innovation. No bureaucrat gets fired for doing things the way there were always done.
- No motivation to reduce costs or keep costs low.
Example: Space X’s dramatic launch cost reduction by actually trying reusable rockets.
See also Why Communism is not discussed in economics.
Non-Profits
Advantages
- can compete with other non-profits
- prices are set equal to average cost
Disadvantages
- prices can not be set to variable cost and average cost are still not pareto optimal
- as non-profits can not make accounting profits either, they have a hard time accessing capital (as they can not pay shareholders for delayed consumption and risk). So they can only take on credits from banks which need to be unexposed to risk so the non profit needs to have enough capital as a security for those loans. They are thus bad at capital expensive tasks.